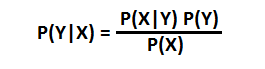What are they?

It is a categorization of classifiers in Bayesian perspective. Recall in Bayes Theorem, we have this formula below:

bayes theorem

Our goal is to find the best **P(Y X).** This reads: Given features X, what is the probability of class Y. Concretely with an example, given that a software engineer lives in Silicon Valley (X), what is the probability he makes over 100K salary (Y), i.e. **P(Y X)**?

Generative Classifiers

A generative classifier tries to learn the model that generates the data behind the scenes by **estimating the assumptions and distributions of the model. It then uses this to predict unseen data, because it assumes the model that was learned captures the real model. As we will see, this is often not true. An example is the Naive Bayes Classifier.

To get **P(Y X)**, generative classifiers do this:
  1. Estimate **P(X Y)** and P(Y) from the data.
  2. Multiply **P(X Y)** and P(Y) according to Bayes Theorem, P(X) is a constant.
  3. Get **P(Y X).**
To continue with our example, a generative classifier first estimate from the data what is the probability a software developer living in Silicon Valley (X) given he makes over 100K (Y), i.e. together it means **P(X Y). Then, it estimates how many software engineers make over 100K, regardless of if he is in Silicon Valley or not, i.e. **P(Y).

Discriminative Classifiers

A discriminative classifier tries to model by just depending on the observed data. It makes fewer assumptions on the distributions but depends heavily on the quality of the data (Is it representative? Are there a lot of data?). An example is the Logistic Regression.

To get **P(Y X)**, discriminative classifiers do this:
  1. Estimate **P(Y X)** from the data.
Yes, only one step. As with our example, a discriminative classifier estimates the probability of a software engineer making over 100K salary given he lives in Silicon Valley, i.e. **P(Y X)**.

When to use a generative classifier or a discriminative classifier?

In practice, discriminative classifiers outperform generative classifiers, if you have a lot of data.

Generative classifiers learn **P(Y X)** indirectly and can get the wrong assumptions of the data distribution. Quoting Vapnik from Statistical Learning Theory:
one should solve the [classification] problem directly and never solve a more general problem as an intermediate step [such as modeling **P(X Y)**].

A very good paper from Andrew Ng in NIPS 2001 concludes that:

a) The generative model does indeed have a higher asymptotic error (as the number of training examples become large) than the discriminative model but,

b) The generative model may also approach its asymptotic error much faster than the discriminative model – possibly with a number of training examples that is only logarithmic, rather than linear, in the number of parameters.

So, simply said, if you have a lot of data, stick with the discriminative models.

 

References: