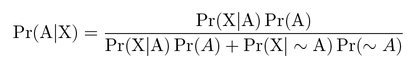Explain to Me : Bayes Theorem
You heard of Bayes Theorem, right? You’ve seen this formula, in some form or others, right?
Yet, you never know what it quite means, and why is it important. Anyway! Forget it after you learnt it, right? Well, I am like you, and here is how I try to understand this thing. Read on!
###
Bayes Theorem is a way to get the real probabilities out of a scenario where true positives (TP), true negatives (TN) , false positives (FP) and false negatives (FN) exist. Rather than seeing a single event, we can see conditions.
We can also think of it as:
P(true probability of an event) = P(true positive) / P(positive)
read as ‘the true probability of an event is equal to the probability of true positives divided by the chance of a positive result‘. P(positive) is actually P(true positive) + P(false positive), as the sum of the probabilities of true positives and false positives equals the probability of observing a positive.
Let’s take an example. There is a cancer test out there. If the patient has cancer, 90% of the times it will return positive result (a true positive). Suppose you took the cancer test, and it returns a positive result.
Does it mean you have 90% chance of having cancer?
You can’t tell, not without knowing 1) what is the probability of people having cancer 2) how many times the cancer test returns positive on a healthy human (false positives).
Now, if you are told that only 1% of the people in the world get cancer, and the cancer test actually returns a positive on a perfectly health human 17% of the time. Using the Bayes formula to help us:
P(you have cancer, given the cancer test returns positive) = P(true positive) / P(positive)
Remembering that:
P(positive) = P(true positive) + P(false positive) = P(TP) + P(FP) :
And simplifying some notion, we have:
**P(cancer positive)**
= P(TP) / ( P(TP) + P(FP) )
**= (P(positive cancer) * P(cancer)) / ( P(positive cancer) * P(cancer) + P(positive no cancer) * P(no cancer) )**
**= (90% * 1%) / (90% * 1% + 17% * (1 – 1%))
= (90% * 1%) / (90% * 1% + 17% * 99%)**
= 5.07%
As it turns out, in this case, you are not having 90% of really having cancer but 5.07% only. Why does the cancer test that can returns positive on people having cancer 90% of the time, actually means you only have 5.07% chance of really getting a cancer?
The intuition is : Even though the test is accurate on cancer patients, but the test get it wrong 17% of the times on healthy humans. Couldn’t you be likely part of the mistaken ones?
So, this is it! Bayes Theorem is just about correcting and measuring the real probabilities of an event given some conditions.
References:
[You heard of Bayes Theorem, right? You’ve seen this formula, in some form or others, right?
Yet, you never know what it quite means, and why is it important. Anyway! Forget it after you learnt it, right? Well, I am like you, and here is how I try to understand this thing. Read on!
###
Bayes Theorem is a way to get the real probabilities out of a scenario where true positives (TP), true negatives (TN) , false positives (FP) and false negatives (FN) exist. Rather than seeing a single event, we can see conditions.
We can also think of it as:
P(true probability of an event) = P(true positive) / P(positive)
read as ‘the true probability of an event is equal to the probability of true positives divided by the chance of a positive result‘. P(positive) is actually P(true positive) + P(false positive), as the sum of the probabilities of true positives and false positives equals the probability of observing a positive.
Let’s take an example. There is a cancer test out there. If the patient has cancer, 90% of the times it will return positive result (a true positive). Suppose you took the cancer test, and it returns a positive result.
Does it mean you have 90% chance of having cancer?
You can’t tell, not without knowing 1) what is the probability of people having cancer 2) how many times the cancer test returns positive on a healthy human (false positives).
Now, if you are told that only 1% of the people in the world get cancer, and the cancer test actually returns a positive on a perfectly health human 17% of the time. Using the Bayes formula to help us:
P(you have cancer, given the cancer test returns positive) = P(true positive) / P(positive)
Remembering that:
P(positive) = P(true positive) + P(false positive) = P(TP) + P(FP) :
And simplifying some notion, we have:
**P(cancer positive)**
= P(TP) / ( P(TP) + P(FP) )
**= (P(positive cancer) * P(cancer)) / ( P(positive cancer) * P(cancer) + P(positive no cancer) * P(no cancer) )**
**= (90% * 1%) / (90% * 1% + 17% * (1 – 1%))
= (90% * 1%) / (90% * 1% + 17% * 99%)**
= 5.07%
As it turns out, in this case, you are not having 90% of really having cancer but 5.07% only. Why does the cancer test that can returns positive on people having cancer 90% of the time, actually means you only have 5.07% chance of really getting a cancer?
The intuition is : Even though the test is accurate on cancer patients, but the test get it wrong 17% of the times on healthy humans. Couldn’t you be likely part of the mistaken ones?
So, this is it! Bayes Theorem is just about correcting and measuring the real probabilities of an event given some conditions.
References:
](http://betterexplained.com/articles/an-intuitive-and-short-explanation-of-bayes-theorem/) [You heard of Bayes Theorem, right? You’ve seen this formula, in some form or others, right?
Yet, you never know what it quite means, and why is it important. Anyway! Forget it after you learnt it, right? Well, I am like you, and here is how I try to understand this thing. Read on!
###
Bayes Theorem is a way to get the real probabilities out of a scenario where true positives (TP), true negatives (TN) , false positives (FP) and false negatives (FN) exist. Rather than seeing a single event, we can see conditions.
We can also think of it as:
P(true probability of an event) = P(true positive) / P(positive)
read as ‘the true probability of an event is equal to the probability of true positives divided by the chance of a positive result‘. P(positive) is actually P(true positive) + P(false positive), as the sum of the probabilities of true positives and false positives equals the probability of observing a positive.
Let’s take an example. There is a cancer test out there. If the patient has cancer, 90% of the times it will return positive result (a true positive). Suppose you took the cancer test, and it returns a positive result.
Does it mean you have 90% chance of having cancer?
You can’t tell, not without knowing 1) what is the probability of people having cancer 2) how many times the cancer test returns positive on a healthy human (false positives).
Now, if you are told that only 1% of the people in the world get cancer, and the cancer test actually returns a positive on a perfectly health human 17% of the time. Using the Bayes formula to help us:
P(you have cancer, given the cancer test returns positive) = P(true positive) / P(positive)
Remembering that:
P(positive) = P(true positive) + P(false positive) = P(TP) + P(FP) :
And simplifying some notion, we have:
**P(cancer positive)**
= P(TP) / ( P(TP) + P(FP) )
**= (P(positive cancer) * P(cancer)) / ( P(positive cancer) * P(cancer) + P(positive no cancer) * P(no cancer) )**
**= (90% * 1%) / (90% * 1% + 17% * (1 – 1%))
= (90% * 1%) / (90% * 1% + 17% * 99%)**
= 5.07%
As it turns out, in this case, you are not having 90% of really having cancer but 5.07% only. Why does the cancer test that can returns positive on people having cancer 90% of the time, actually means you only have 5.07% chance of really getting a cancer?
The intuition is : Even though the test is accurate on cancer patients, but the test get it wrong 17% of the times on healthy humans. Couldn’t you be likely part of the mistaken ones?
So, this is it! Bayes Theorem is just about correcting and measuring the real probabilities of an event given some conditions.
References:
[You heard of Bayes Theorem, right? You’ve seen this formula, in some form or others, right?
Yet, you never know what it quite means, and why is it important. Anyway! Forget it after you learnt it, right? Well, I am like you, and here is how I try to understand this thing. Read on!
###
Bayes Theorem is a way to get the real probabilities out of a scenario where true positives (TP), true negatives (TN) , false positives (FP) and false negatives (FN) exist. Rather than seeing a single event, we can see conditions.
We can also think of it as:
P(true probability of an event) = P(true positive) / P(positive)
read as ‘the true probability of an event is equal to the probability of true positives divided by the chance of a positive result‘. P(positive) is actually P(true positive) + P(false positive), as the sum of the probabilities of true positives and false positives equals the probability of observing a positive.
Let’s take an example. There is a cancer test out there. If the patient has cancer, 90% of the times it will return positive result (a true positive). Suppose you took the cancer test, and it returns a positive result.
Does it mean you have 90% chance of having cancer?
You can’t tell, not without knowing 1) what is the probability of people having cancer 2) how many times the cancer test returns positive on a healthy human (false positives).
Now, if you are told that only 1% of the people in the world get cancer, and the cancer test actually returns a positive on a perfectly health human 17% of the time. Using the Bayes formula to help us:
P(you have cancer, given the cancer test returns positive) = P(true positive) / P(positive)
Remembering that:
P(positive) = P(true positive) + P(false positive) = P(TP) + P(FP) :
And simplifying some notion, we have:
**P(cancer positive)**
= P(TP) / ( P(TP) + P(FP) )
**= (P(positive cancer) * P(cancer)) / ( P(positive cancer) * P(cancer) + P(positive no cancer) * P(no cancer) )**
**= (90% * 1%) / (90% * 1% + 17% * (1 – 1%))
= (90% * 1%) / (90% * 1% + 17% * 99%)**
= 5.07%
As it turns out, in this case, you are not having 90% of really having cancer but 5.07% only. Why does the cancer test that can returns positive on people having cancer 90% of the time, actually means you only have 5.07% chance of really getting a cancer?
The intuition is : Even though the test is accurate on cancer patients, but the test get it wrong 17% of the times on healthy humans. Couldn’t you be likely part of the mistaken ones?
So, this is it! Bayes Theorem is just about correcting and measuring the real probabilities of an event given some conditions.
References:
](http://betterexplained.com/articles/an-intuitive-and-short-explanation-of-bayes-theorem/)](http://yudkowsky.net/rational/bayes) http://lesswrong.com/lw/2b0/bayes_theorem_illustrated_my_way/