Why do We Need a Bias Neuron?
Have you wondered why there is always a bias neuron in a perceptron, neural network? Does the algorithm work without a bias neuron? If yes, or no, either way, have you wondered why?
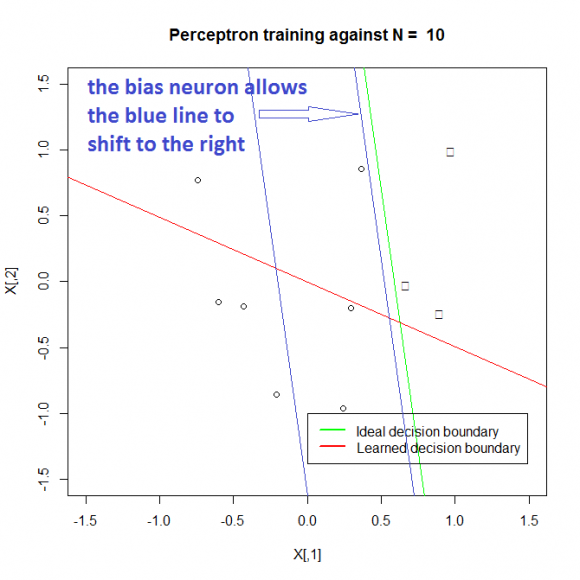
A bias neuron allows a classifier to shift the decision boundary left or right. In an algebraic term, the bias neuron allows a classifier to translate its decision boundary. To translation is to “move every point a constant distance in a specified direction”.
Now, let’s illustrate with an example. Consider a 2D perceptron trying to classify 10 points below.
Points that fall on the right side of the ideal decision boundary (green in picture) should be classified as +1, while all points on the left of the green line as -1.
We are going to train a 2D perceptron without bias to classify the 10 points. Without the bias neuron, the perceptron is unable to shift the blue decision boundary on the left to the blue decision boundary on the right, thus being never able to learn the ideal decision boundary or the closest match (the blue decision boundary on the right). The result is the learned decision boundary (red line) which must pass through the origin (0,0), has failed to classify some of the points. Notice that since the red line must pass through the origin due to having no bias neuron, however you rotate the red line, it will always fail to classify some points. The only solution is to shift the decision boundary to the right to where the blue decision boundary is.
You may find the code in R that demonstrates 1) how a perceptron will learn a decision boundary 2) how a perceptron fails to learn a decision boundary in this repository.